Tugas SPK Program Linear Maksimasi

Soal :

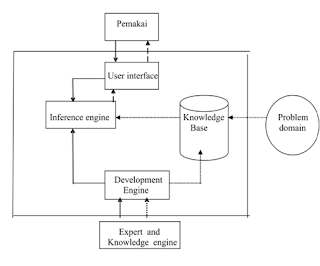
. Suatu perusahaan akan memproduksi 2 jenis produk yaitu lemari dan kursi. Untuk memproduksi 2 produk tersebut di butuhkan 2 kegiatan yaitu proses perakitan dan pengecatan. Perusahaan menyediakan waktu 56 jam untuk proses perakitan dan 60 jam untuk proses pengecatan. Untuk produksi 1 unit lemari diperlukan waktu 8 jam perakitan dan 5 jam pengecatan. Untuk produksi 1 unit kursi diperlukan 7 jam perakitan dan 12 jam pengecatan. Jika masing masing produk adalan Rp. 200 ribu untuk lemari dan 100 ribu untuk kursi. Tentukan solusi optimal agar mendapatkan untuk masimal.

Penyelesaian :

A. Pembentukan Fungsi Tujuan da Fungsi Kendala

    Lemari X

    Kursi   Y

Produk	Perakitan	Pengecatan	Harga/unit
Lemari (x)	8 Jam	5 Jam	200
Kursi    (y)	7 Jam	12 Jam	100
Waktu yang disediakan	56 Jam	60 Jam

    Fungsi Tujuan :

    Z = 200x + 100y

    Fungsi Kendala : 

   (I)  8x + 7y ≤ 56

   (II) 5x + 12y ≤ 60 

B. Menentukan Titik Potong

    Untuk Persamaan (I)

    Jika x = 0                                    Jika y = 0                                             

      8x + 7y = 56                               8x + 7y = 56                               

      8(0) + 7y = 56                            8x + 7(0) = 56                          

                7y = 56                             8x = 56                                             

                  y = 56/7                            x = 56/8                                            

                  y = 8                                  x = 7                                               

    Titik Potong { 0,8}                    Titik Potong { 7,0}

    Untuk Persamaan (II)

    Jika x = 0                                    Jika y = 0

    5x + 12y = 60                             5x + 12y = 60
    5(0) + 12y = 60                          5x + 12(0) = 60
              12 y = 60/12                     5x = 60
                  y = 60                            x = 60/5
                  y = 5                              x = 12
    Titik Potong {0,5}                    Titik Potong {12,0}

C. Gambar Grafiknya sebagai berikut :

 D. Mencari nilai B dengan melakukan Eliminasi :

       5x + 12y = 60

       5x + 12(3,3) = 60

       5x +  39,6    = 60

       5x = 60 - 39,6

       5x = 20,4

         x = 20,4/5

         x = 4,08

Hasil nilai B { 4,08 , 3,3}

E. Penentuan Solusi 

    Untuk Titik A { 0,8 }

    Z = 200x + 100y

    Z = 200(0) + 100(8)

    Z = 0 + 800  

    Z = 800

    Untuk Titik B { 4,08 , 3,3 } 

     Z = 200x + 100y

     Z = 200(4,08) + 100(3,3)

     Z = 816 + 330  

     Z = 1146                   

     Untuk Titik C { 7,0 }

     Z = 200x + 100y

     Z = 200(7) + 100(0) 

     Z = 1400 + 0

     Z = 1400 

Maka dapat disimpulkan nilai maksimum ada di titik B { 4,08 , 3,3 } yaitu 1146

Klasifikasi Sistem Pendukung Keputusan (Desicion Support System)

Institutional vs adhoc

Donovan dan Madnick (1977) menunjukkan bahwa arti DSS dapat diklasifikasikan sebagai "institutional" atau "ad hoc" tergantung pada karakteristik tertentu dari keputusan yang didukung. DSS yang berhubungan dengan keputusan yang bersifat berulang dianggap institutional, sedangkan ad hoc DSS berhugungan dengan keputusan spesifik yang biasanya tidak terantisipasi sebelumnya. Menurut Donovan dan Madnick (1977), DSS institutional yang paling sesuai untuk aplikasi pengendalian operasional, sedangkan ad hoc yang paling sesuai dengan aplikasi perencanaan strategis.

Personal support, group support, atau organizational support
Hackathorn dan Keen [1981], membedakan sistem berbasis komputer dalam 3 kategori: individual, group dan organisasi.

Organizational DSS adalah sistem pendukung keputusan yang difokuskan pada tugas-tugas organisatori atau kegiatan yang melibatkan banyak proses dan pelaku, misalnya:

1. Mengembangkan Rencana Pemasaran
2. Anggaran Biaya Negara,

dimana kegiatan individual harus berjalan harmonis dan saling mendukung dengan individu yang lain. Komputer dipakai sebagai jembatan untuk komunikasi dan koordinasi disamping juga untuk membantu memecahkan masalah.



GSS v. Individual DSS

Watson [1990]: Kombinasi dari komputer dan teknologi informasi, yang dirancang untuk koordinasi dan mendistribusikan pengambilan keputusan melalui area fungsional dan layer-layer hirarkie sehingga pengambilan keputusan dapat sejalan dengan tujuan dari organisasi .

Carter [1992]: DSS yang dipakai oleh individu atau kelompok, dalam banyak workstation dalam lebih dari 1 unit organisasi yang membuat banyak keputusan yang otonom tapi saling terkait.

Sehingga secara umum, karakter dari ODSS adalah:


1. Fokus dari ODSS adalah tugas-tugas organisasi atau keputusan yang mempengaruhi banyak unit organisasi atau perusahaan
2. ODSS beroperasi dalam lintas layer hirarkie
3. ODSS melibatkan sistem berbasis komputer dan teknologi komunikasi.


Ada beberapa perbedaan antara ODSS dengan DSS yang standar

1. Case management
Case management digunakan untuk membantu user yang ingin menjalankan suatu model beberapa kali untuk pengambilan keputusan yang serupa. Case didefinisikan sebagai skenario khusus dari suatu model. Case meliputi spesifikasi dari semua input data yang digunakan dalam skenario tsb. CMS (Case Management System) melakukan 3 hal utama:


1. Berperilaku seperti sistem akuntansi untuk skenario yang dibuat oleh user, menfasilitasi pembuatan, penugasan, penyalinan, dokumentasi dan katalog dari case model.

2. Meyediakan cara yang mudah untuk memodifikasi data input dari suatu model untuk suatu skenario. Dimana perbedaan penggunaan input akan menghasilkan output yang berbeda untuk skenario yang sama.

3. Dapat memberikan perbandingan output untuk beberapa skenario yang telah dijalankan,



2. DSS aksesibel untuk banyak user pada banyak lokasi melalui Lan atau WAN

Custom made vs vendor ready made

Jika semula upaya penggunaan teknologi informasi selalu identik dengan pengembangan aplikasi dari awal yang tentunya membutuhkan waktu, saat ini konsumen cenderung untuk memilih menggunakan aplikasi-aplikasi yang telah tersedia di pasaran yang sesuai dengan kebutuhannya. Hal ini diharapkan akan dapat meminimalkan biaya dan waktu yang dibutuhkan dalam implementasi teknologi informasi.


Terdapat beberapa jenis DSS berdasarkan klasifikasi diantaranya yaitu custom made dan juga ready made :


Pengertian Custom-made yaitu
· membuat sebuah pesanan sesuai dengan spesifikasi pelanggan atau individu
· membuat khusus untuk sebuah tujuan tertentu
· suatu sistem yang dibuat sesuai dengan spesifikasi masing-masing
· suatu sistem yang dikembangkan hanya untuk memenuhi kebutuhan spesifik dari satu instansi atau industri tertentu.


Beberapa ciri Custom-made System :
· butuh waktu yang relatif lama untuk pengembangan
· pengembangan dari awal
· spesifik hanya untuk industri tertentu
· setiap unit memiliki option pengembangan sendiri-sendiri dan sulit diintegrasikan
 
Pengertian Ready-made yaitu
· aplikasi telah tersedia dan siap pakai
· suatu sistem informasi yang dikembangkan oleh vendor tertentu untuk memenuhi kebutuhan dari berbagai macam proses bisnis


Beberapa ciri Ready-made System :
· aplikasi telah tersedia
· hanya diperlukan modifikasi dalam pengembangannya
· dokumentasi adalah bagian dari aplikasi
· aplikasi telah didesain secara terintegrasi
· waktu pengembangan dan implementasi relatif lebih cepat
· efisiensi dalam pemanfaatan SDM, pengguna hanya difokuskan untuk operasi dan pemeliharaan aplikasi saja
· biaya relatif lebih mahal karena sebagian besar proses pengembangan dilakukan oleh pihak vendor




SIKLUS HIDUP SISTEM (WATERFALL APPROACH)


Siklus hidup system adalah proses evolusioner yang diikuti dalam menerapkan system atau subsistem informasi berbasis komputer. Siklus hidup system terdiri dari serangkaian tugas yang erat yang mengikuti langkah-langkah pendekatan system. Karena tugas-tugas tersebut mengikuti suatu pola yang teratur dan dilakukan top-down, sering disebut sebagai pendekatan air terjun (waterfall approach) bagi pengembangan dan penggunaan system.


Pengelolaan Siklus Hidup

Siklus hidup system yang pertama dikelola oleh manajer unit jasa informasi, dibantu oleh manajer dari analis system, pemrograman dan operasi.


q Tanggung jawab eksekutif


Ketika system memiliki nilai strategis atau mempengaruhi seluruh organisasi, direktur utama atau komite eksekutif mungkin memutuskan untuk mengawasi proyek pengembangannya.


q Komite Pengarah SIM


Banyak perusahaan membuat komite khusus, dibawah tingkat komite eksekutif, yang bertanggung jawab atas pengawasan seluruh proyek system, yakni komite pengarah. Tujuan komite tersebut memberikan petunjuk, pengarahan, dan pengendalian yang berkesinambungan terhadap penggunaan sumber daya komputer perusahaan. Komite pengarah SIM melaksanakan tiga fungsi utama:


· Menetapkan kebijakan yang memastikan dukungan komputer untuk mencapai tujuan strategis perusahaan.


· Menjadi pengendali keuangan dengan bertindak sebagai badan yang berwenang memberi persetujuan bagi semua permintaan dana yang berhubungan dengan komputer


· Menyelesaikan pertentangan yang timbul sehubungan dengan prioritas penggunaan komputer.


q Kepemimpinan proyek


Tim proyek meliputi semua orang yang ikut serta dalam pengembangan system berbasis komputer. Sebuah tim terdiri dari pemakai, spesialis informasi, dan juga auditor internal. Auditor memastikan bahwa rancangan system memenuhi persyaratan


tertentu dalam hal akurasi, pengendalian, keamanan dan dapat di audit. Tim proyek tidak berkelanjutan dan biasanya dibubarkan ketika penerapan system selesai.




Tahap-tahap Siklus Hidup Sistem


A. Tahap Perencanaan


Keuntungan yang dapat diperoleh dari merencanakan suatu proyek CBIS:


· Menentukan lingkup proyek


· Mengenali berbagai area permasalahan potensial


· Mengatur urutan tugas


· Memberikan dasar untuk pengendalian


Langkah-langkah dalam tahap perencanaan:


1. Menyadari masalah
2. Mendefinisikan masalah
3. Menentukan tujuan system
4. Identifikasi Kendala/Batasan system
5. Membuat studi kelayakan
6. Usulan penelitian system
7. Menyetujui atau menolak penelitian proyek
8. Menetapkan mekanisme pengendalian




Memantau kemajuan proyek
Setelah jadwal proyek ditetapkan, jadwal itu harus didokumentasikan dalam bentuk yang memudahkan pengendalian. Berbagai teknik dokumentasi dapat digunakan, termasuk berbagai jenis table, grafik, dan diagram.






B. Tahap Analisis
Analis sistem adalah penelitian atas system yang telah ada dengan tujuan untuk merancang system baru atau diperbarui. Langkah-langkah dalam tahap analisis:

1. Mengumumkan Penelitian Sistem
2. Mengorganisasikan tim proyek
3. Mendefinisikan kebutuhan informasi
4. Mendefinisikan Kriteria Kinerja Sistem
5. Menyiapkan usulan rancangan
6. Menyetujui atau menolak Rancangan Proyek

C. Tahap Perancangan
Rancangan system adalah penentuan proses dan data yang diperlukan oleh system baru. Jika system itu berbasis komputer, rancangan dapat menyertakan spesifikasi jenis peralatan yang akan digunakan. Langkah-langkah dalam tahap perancangan:


1. Merancang system yang terinci
2. Mengidentifikasi berbagai alternatif konfigurasi sistem
3. Mengevaluasi berbagai alternatif konfigurasi system
4. Memilih Konfigurasi terbaik
5. Menyiapkan usulan penerapan
6. Menyetujui atau menolak Penerapan sistem



D. Tahap Implementasi

Implementasi menerapkan kegiatan dan mengintegrasikan sumber daya fisik dan konseptual yang menghasilkan suatu system bekerja. Langkah-langkah dalam tahap Implementasi:
1. Merencanakan penerapan
2. Mengumumkan penerapan
3. mendapatkan sumber daya perangkat keras
4. Mendapatkan sumber daya perangkat lunak
5. Menyiapkan database
6. Menyiapkan fasilitas fisik
7. Mendidik Peserta dan pemakai
8. Menyiapkan usulan cutover
9. Menyetujui atau menolak masuk ke system yang baru
10. Masuk ke system yang baru (cutover)


F Percontohan (Pilot)
Sistem percobaan yang diterapkan dalam satu subset dari keseluruhan operasi, seperti pada kantor atau daerah tertentu. Jika percontohan ini sukses, system akan diterapkan pada operasi selebihnya, dengan menggunakan salah satu dari tiga pendekatan cutover lainnya

F Serentak (Immediate)
Beralih dari system lama ke system baru pada saat yang ditentukan. Pendekatan ini layak pada system yang kecil, karena permasalahan waktu semakin besar jika skala operasi meningkat.


G Bertahap(Phased)
Sistem baru digunakan berdasarkan bagian per bagian pada suatu waktu. Cutover bertahap lebih popular untuk system berskala besar.


H Paralel(Parallel)
Sistem lama dipertahankan sampai system baru telah diperiksa secara menyeluruh. Pendekatan ini memberikan pengamanan yang paling baik terhadap kegagalan tetapi yang paling mahal karena kedua sumber daya harus dipertahankan.

Artikel Mengenai Sistem Pendukung Keputusan

Sistem Pendukung Keputusan

Sistem informasi  komputer yang dipergunakan untuk memecahkan permasalahan spsesifik, mampu berkomunikasi dalam memecahkan masalah semiterstruktur. Informasi dihasilkan dalam bentuk laporan periodik dan khusus, output dari model matematika dan sistem pakar serta menggunakan beberapa jenis grafik. Komunikasi dilakukan pada saat berbagai kelompok manajer terlibat dalam pemecahan masalah.

Gambar Sistem pendukung keputusan

Perangkat Lunak > menghasilkan laporan periodik ( yang disiapkan sesuai jadwal ) dan laporan khusus ( yang disiapkan sebagai jawaban atas kebutuhan informasi yang tak terduga )

Model matematika > menghasilkan informasi sebagai hasil dari simulasi yang melibatkan satu atau beberapa komponen dari sistem fisik perusahaan atau berbagai aspek operasinya.

Perangkat Lunak Group Decision Support System >  memungkinkan beberapa pemecah masalah bekerja sama dan saling berkomunikasi untuk memperoleh solusi.

OTOMATIS KANTOR

OK > sistem informasi  komputer yang mencakup semua sistem elektronik baik formal maupun informal, sistem formal ialah sistem yang bersifat  prosedural dengan menggunakan dokumentasi, tulisan maupun uraian, sedangkan sistem  informal ialah sistem tidak terencana sehingga tanpa dukungan dokumentasi tetapi cukup dengan lisan. Otomatis kantor berkaitan dengan komunikasi informasi didalam maupun diluar perusahaan, dan kebanyakan dipergunakan oleh orang yang bekerja didalam kantor ( pegawai administrasi, karyawan, sekretaris, profesional, manajer ).

Gambar Sistem otomatis kantor

Informasi dikumpulkan dari sistem fisik perusahaan pada bagian bawah, sedangkan informasi berfungsi sebagai input bagi aplikasi otomatis kantor berbasis komputer seperti pengolah kata, surat elektronik dan konferensi komputer serta memungkinkan pemecah masalah saling berkomunikasi dengan menggunakan komputer mereka masing - masing.

SISTEM PAKAR

Sistem Pakar memiliki potensi untuk memperluas kemampuan pemecahan masalah manajer melebihi kemampuan normalnya. Sistem pakar terdiri dari empat bagian utama : User interface Penggunaan input dan output multimedia yang sekarang mendapatkan perhatian dari pengembang sistem sebagai cara untuk meningkatkan komunikasi antar komputer dan pemakai., Knowledge base menggunakan metode - metode pemecahan masalah dan menggunakan formula untuk mengekspresikan logika masalah, Inference engine menggunakan penalaran menyerupai manusia didalam memformulasikan isi daripada Knowledge base, dan Development engine berisi tentang bahasa pemrograman untuk pengembangan sistem pakar.

Gambar Sistem pakar

Sistem pakar terdiri dari empat bagian antara lain User interface yang memungkinkan pemakai berinteraksi dengan sistem pakar. Knowledge base menyimpan akumulasi pengetahuan dari masalah tertentu yang akan diselesaikan. Inference engine menyediakan kemamapuan penalaran yang menafsirkan isi knowlegde base. Pakar dan analisis sistem menggunakan development engine untuk menciptakan sistem pakar.